Calcula la desviación estándar basándose en toda la población, incluidos valores lógicos y texto. La desviación estándar es una medida de la dispersión de los valores con respecto al valor promedio (la media).

Sintaxis

STDEVPA(valor1,valor2,...)

Valor1,valor2,...   son entre 1 y 30 valores correspondientes a una población.

Comentarios

• STDEVPA supone que sus argumentos son toda la población. Si los datos representan una muestra de la población, calcule la desviación estándar mediante la función STDEVA.
• Los argumentos que contienen TRUE devuelven 1; los argumentos que contienen texto o FALSE devuelven 0 (cero). Si el cálculo no debe incluir texto ni valores lógicos, use la función STDEVP.
• En el caso de muestras de gran tamaño, STDEVA y STDEVPA devuelven valores aproximadamente iguales.
• La desviación estándar se calcula con el método "sesgado" o "n".
• STDEVPA usa la siguiente fórmula:

  

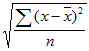
Ejemplo