Calcula la desviación estándar basándose en una muestra. La desviación estándar es una medida de la dispersión de los valores con respecto al valor promedio (la media). En el cálculo se incluyen los valores de texto y los valores lógicos TRUE y FALSE.

Sintaxis

STDEVA(valor1,valor2,...)

Valor1,valor2,...   son entre 1 y 30 valores correspondientes a una muestra de la población.

Comentarios

• STDEVA supone que sus argumentos son una muestra de la población. Si los datos representan toda la población, calcule la desviación estándar mediante la función STDEVPA.
• Los argumentos que contienen TRUE devuelven 1; los argumentos que contienen texto o FALSE devuelven 0 (cero). Si el cálculo no debe incluir texto ni valores lógicos, use la función de hoja de cálculo STDEV.
• La desviación estándar se calcula con el método "no sesgado" o "n-1".
• STDEVA usa la siguiente fórmula:

  

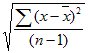
Ejemplo

Supongamos que 10 herramientas troqueladas en la misma máquina durante el mismo proceso de producción son elegidas como una muestra aleatoria y medimos su resistencia a la ruptura.