Devuelve la distribución hipergeométrica. HYPGEOMDIST devuelve la probabilidad de un número determinado de éxitos de la muestra, dados el tamaño de la muestra, los éxitos de la población y el tamaño de la población. Use HYPGEOMDIST para problemas con una población finita, donde cada observación es un éxito o un error y donde cada subconjunto de un tamaño dado se elige con la misma probabilidad.

Sintaxis

HYPGEOMDIST(muestra_éxito,núm_de_muestra,población_éxito,núm_de_población)

Muestra_éxito   es el número de éxitos en la muestra.

Núm_de_muestra   es el tamaño de la muestra.

Población_éxito   es el número de éxitos en la población.

Núm_de_población   es el tamaño de la población.

Comentarios

• Todos los argumentos se truncan en enteros.
• Si algún argumento no es numérico, HYPGEOMDIST devuelve el valor de error #¡VALOR!.
• Si muestra_éxito < 0 ó es mayor que el menor valor de núm_de_muestra o población_éxito, HYPGEOMDIST devuelve el valor de error #¡NUM!.
• Si muestra_éxito es menor que el mayor valor de 0 ó (núm_de_muestra - núm_de_población + población_éxito), HYPGEOMDIST devuelve el valor de error #¡NUM!.
• Si núm_de_muestra < 0 ó > núm_de_población, HYPGEOMDIST devuelve el valor de error #¡NUM!.
• Si población_éxito < 0 ó > núm_de_población, HYPGEOMDIST devuelve el valor de error #¡NUM!.
• Si núm_de_población < 0, HYPGEOMDIST devuelve el valor de error #¡NUM!.
• La ecuación de la distribución hipergeométrica es:

  

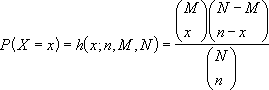
  donde:

  x = muestra_éxito

  n = núm_de_muestra

  M = población_éxito

  N = núm_de_población

HYPGEOMDIST se usa en los muestreos sin reemplazo de una población finita.

Ejemplo

Una muestra de bombones contiene 20 unidades. Ocho unidades son de caramelo y las 12 restantes son de nueces. Si una persona elige aleatoriamente 4 unidades, la siguiente función devuelve la probabilidad de que exactamente 1 unidad sea un bombón de caramelo.