Devuelve el intervalo de confianza para una media de la población con una distribución normal. El intervalo de confianza es un intervalo a ambos lados de la media de una muestra. Por ejemplo, si se realiza el pedido de un producto a través del correo, se puede determinar, con un nivel de confianza concreto, la fecha más temprana y más tardía en la que llegará el producto.
Sintaxis
CONFIDENCE(alfa,desv_estándar,tamaño)
Alfa es el nivel de significancia usado para calcular el nivel de confianza. El nivel de confianza es igual a 100*(1 - alfa)%; en otras palabras, un valor de alfa de 0,05 indica un nivel de confianza de un 95 por ciento.
Desv_estándar es la desviación estándar de la población para el rango de datos y se supone que se conoce su valor.
Tamaño es el tamaño de la muestra.
Comentarios
- Si algún argumento no es numérico, CONFIDENCE devuelve el valor de error #¡VALOR!.
- Si alfa ≤ 0 ó ≥ 1, CONFIDENCE devuelve el valor de error #¡NUM!.
- Si desv_estándar ≤ 0, CONFIDENCE devuelve el valor de error #¡NUM!.
- Si el valor de tamaño no es un entero, se truncará.
- Si el valor de tamaño < 1, CONFIDENCE devolverá el valor de error #¡NUM!.
- Si suponemos que el valor de alfa es 0,05, debemos calcular el área debajo de la curva normal estándar igual a (1 - alfa), o bien, 95 por ciento. Este valor es ± 1,96. Por consiguiente, el intervalo de confianza es:
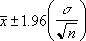
Ejemplo
Supongamos que observamos que, en nuestra muestra de 50 personas que viajan diariamente a su lugar de trabajo, el tiempo medio de viaje es de 30 minutos con una desviación estándar de la población de 2,5. Podremos confiar con un 95% en que la media de la población se encuentra dentro del intervalo:
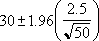
| Alfa | Desv_estándar | Tamaño | Fórmula |
Descripción (Resultado) |
| 0,05 | ,5 | 50 | =CONFIDENCE([Alfa],[Desv_estándar],[Tamaño]) |
Intervalo de confianza para una media de la población. En otras palabras, la duración media de viaje al trabajo es de 30 ± 0,692951 minutos, o bien, de 29,3 a 30,7 minutos. (0,692951) |